ML From Scratch, Part 1: Linear Regression

Statistical Motivation

In this section we will use statistical considerations to motivate the definition of a particular mathematical optimization problem. Once we have posed this problem, we will afterwards ignore the statistics altogether and focus on numerical methods for solving the optimization problem.

Let’s start by deriving the so-called normal equation from a statistical model. Let’s say that \(X\) is a random vector of length \(m\) and \(Y\) is a scalar random variable. \(X\) and \(Y\) are not independent, but have a joint probability distribution \(F(x, y; \Theta, \sigma)\) parameterized by a non-random parameter vector \(\Theta\), a non-negative scalar \(\sigma\), and a random error term \(\epsilon \sim \mathcal{N}(0, \sigma^2)\). The model is:

\[ Y = X^T \Theta + \epsilon \]

Now suppose we sample \(n\) independent observations from \(F\). We place these into a real-valued \(n\times m\) matrix \(\mathbf{X}\) and a real-valued vector \(\mathbf{y}\). Just to be absolutely clear, \(\mathbf{X}\) and \(\mathbf{y}\) are not random variables; they are the given data used to fit the model. We can then ask, what is the likelihood of obtaining the data \((\mathbf{X}, \mathbf{y})\) given a parameter vector \(\Theta\)? By rearranging our equation as \(Y - X\cdot\Theta = \epsilon \sim \mathcal{N}(0, \sigma^2)\) and using the p.d.f. of the normal distribution, we can see that:

\[ \begin{align} L(\Theta;\mathbf{X},\mathbf{y}) & = P(\mathbf{X},\mathbf{y};\Theta) \\ & = \prod_{i=1}^{n} P(\mathbf{X}_i,\mathbf{y}_i;\Theta) \\ & = \prod_{i=1}^{n} \frac{1}{\sqrt{2\pi}\sigma} \text{exp}\Big(\frac{-(\mathbf{y}_i - \mathbf{X}_i^T\Theta)^2}{2\sigma^2} \Big) \\ \end{align} \]

That looks pretty awful, but there are a couple easy things we can do to make it a look a lot simpler. First, that constant term out front doesn’t matter at all: let’s just call it \(C\) or something. We can also take that \(e^{-2\sigma^2}\) outside the product as \(e^{-2N\sigma^2}\), which we’ll also stuff into the constant \(C\) because we’re only interested in \(\Theta\) right now. Finally, we can take a log to get rid of the exponential and turn the product into a sum. All together, we get the log-likelihood expression:

\[ \begin{align} \ell(\Theta;\mathbf{X},\mathbf{y}) & = \log L(\Theta;\mathbf{X},\mathbf{y}) \\ & = C - \sum_{i=1}^N -(\mathbf{y}_i - \mathbf{X}^T_i\Theta)^2 \\ & = C - \lVert\mathbf{y} - \mathbf{X}\Theta\rVert^2 \\ \end{align} \]

Now, because log is a monotonically increasing function, maximizing \(\ell\) is the same as maximizing \(L\). Furthermore, the constant \(C\) has no effect whatsoever on the location of the maximum. We can also remove the minus sign and consider the problem as a minimization problem instead. Therefore our maximum likelihood estimate of \(\Theta\) for a given data set \((X, y)\) is simply:

\[ \hat{\Theta} \triangleq \underset{\Theta}{\text{argmin}} \, \lVert\mathbf{y} - \mathbf{X}\Theta\rVert^2 \]

If statistics isn’t really your thing, I have some good news for you: we’re quits with it. Everything in this final equation is now a real-valued vector or matrix: there’s not a random variable or probability distribution in sight. It’s all over except for the linear algebra.

What we did above was essentially a short sketch of the relevant parts of the Gauss-Markov theorem. In particular, we’ve shown that the OLS solution to \(\mathbf{y} - \mathbf{X}\Theta\) is the Maximum Likelihood Estimate for the parameters of the particular statistical model we started with. This isn’t true in general, but it is exactly true for linear regression with a normally distributed error term. The full Gauss-Markov theorem proves a bunch of other nice properties: for example, it turns out this estimator is unbiased and we can even say that it’s optimal in the sense that it is the best possible linear unbiased estimator. But we won’t need these further theoretical results to implement a working model.

If there’s one thing you should remember, it’s this: the fact that the p.d.f. of the Gaussian distribution has the quadratic term \((x -\mu)^2\) in the exponent is the reason why squared error is the “right” loss function for linear regression. If the error of our linear model had a different distribution, we’d have to make a different choice.

Our key takeaway is that if it’s true that our response variable is related to our predictor variables by a linear equation plus a certain amount of random Gaussian noise, then we can recover good, unbiased estimates of that linear equations coefficients from nothing more than a finite number of data points sampled from the underlying distribution, and the way to actually calculate those estimates is to solve the OLS problem for the data set.

Ordinary Least Squares

Note: for this next section, we’re going to be doing some light vector calculus. I suggest you reference the matrix cookbook if any of the notation or concepts aren’t familiar.

Let’s call the right-hand side (the part we’re trying to minimize) \(J\). Then we have:

\[ J(\Theta) = \lVert \mathbf{y} - \mathbf{X}\Theta \rVert^2 \]

And the problem is to minimize \(J\) with respect to \(\Theta\). As optimization problems go, this one is pretty well behaved: it’s continuous, quadratic, convex, everywhere continuously differentiable, and unconstrained. That’s a fancy way of saying that it’s shaped like a big, round bowl. A bowl has a unique lowest point and it can always be found simply by letting a marble roll down hill until it comes to rest exactly at the lowest point.

Because of these nice properties (and a very useful set of theorems called the KKT conditions) we know that these properties guarentee that \(J\) has a unique global minimum and that we can find the minimum - the bottom of the bowl - by finding the one place where the gradient is zero in all directions.

Now, it may not be obvious at first how to take the gradient of the squared norm of a vector, but recall that it is the inner product of that vector with its dual:

\[ \nabla_\Theta J = \nabla_\Theta \; (\mathbf{y} - \mathbf{X}\Theta)^T(\mathbf{y} - \mathbf{X}\Theta) \]

Expanding it out with FOIL:

\[ \nabla_\Theta J = \nabla_\Theta \; ( \mathbf{y}^T \mathbf{y} - (\mathbf{X}\Theta)^T \mathbf{y} - \mathbf{y}^T \mathbf{X}\Theta + \Theta^T (\mathbf{X}^T \mathbf{X}) \Theta ) \]

It’s obvious that \(\mathbf{y}^T \mathbf{y}\) is constant with respect to \(\Theta\) so the first term simply vanishes. It’s less obvious but also true that the next two terms are equal to each other - just remember that a J is a scalar, so those terms are each scalar, and the transpose of a scalar is itself. The final term is a quadratic form, and the general rule is $ x^T A x = A^T x + A x $ but because the product of a matrix with itself is always symmetric (\(X^T X = (X^T X)^T\)) we can use the simpler form \(\nabla x^T A x = 2 A x\).

\[ \nabla_\Theta J = - 2 \mathbf{X}^T \mathbf{y} + 2 \mathbf{X}^T \mathbf{X} \Theta \]

Setting this equal to zero at the minimum, which we will call \(\hat{\Theta}\), and dividing both sides by two, we get:

\[ \mathbf{X}^T \mathbf{X} \hat{\Theta} = \mathbf{X}^T \mathbf{y} \tag{1} \]

This is the so-called normal equation. The importance of this step is that we’ve reduced the original optimization problem to a system of linear equations which may be solved purely by the methods of linear algegra. To see this, note that we know \(\mathbf{X}\) and \(\mathbf{y}\), so the right hand side is a known vector, the left-hand side is a matrix times an unknown vector, so this is just the familiar equation for solving for a particular solution to a system of equations \(Ax = b\).

Because \(\mathbf{X}^T \mathbf{X}\) is square and non-singular and therefore invertible, we could just left-multiply both sides by its inverse to get an explicit closed form for \(\hat{\Theta}\):

\[ \hat{\Theta} = (\mathbf{X}^T \mathbf{X})^{-1} X^T \mathbf{y} \]

However, it turns out there is a faster and more numerically stable way of solving for \(\hat{\Theta}\) which relies on the QR Decomposition of the matrix \(\mathbf{X}\).

QR Decomposition

Since we’re going to be both implementing and relying on the QR decomposition in a minute, it’s worth making sure we understand how it works in detail. A QR decomposition of a matrix square \(A\) is a product of an orthogonal matrix \(Q\) and an upper-triangular matrix \(R\) such that \(A = QR\). It always exists and there’s a reasonably performant algorithm for calculating it. Why is it beneficial to put a matrix in this form? In short, because it makes it very easy to compute solutions to systems of equations in matrix form \(Ax = b\); all we have to do is compute \(A = QR\) and write the problem as \(R x = Q^{-1} b\) which is easy to compute. Let’s examine those two steps in more detail.

Why is \(Q\) easy to invert? Recall that \(Q\) is orthogonal which implies that \(Q^{-1} = Q^T\). Most linear algebra libraries don’t even have to explicitly copy a matrix to take a transpose but simply set a flag that indicates that from now on it will operate on it row-wise instead of column-wise or vice versa. That means taking a transpose is free for all intents and purposes.

Why is \(Rx = Q^T b\) easy to solve? Well, the right-hand side is just a vector. R is upper triangular, so we can solve this with a technique called back-substitution. Back-substitution is easiest to explain with an example. Consider this system of equations in matrix form, where the matrix is upper-triangular:

\[ \begin{bmatrix} 2 & 1 & 3 \\\ 0 & 1 & 1 \\ 0 & 0 & 4 \\ \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ \end{bmatrix} = \begin{bmatrix} 2 \\ 2 \\ 8 \\ \end{bmatrix} \]

We start on the bottom row, which is simply an equation \(4x_3 = 8\), so \(x_3 = 2\). The second row represents the equation \(x_2 + x_3 =2\), but we already know \(x_3\), so we can substitute that back in to get \(x_2 - 2 = 0\), so \(x_2 = 0\). The top row is \(2x_1 + x_2 + 3_x3 = 2x_1 + 6 = 2\), so \(x_1 = -2\). This is back-substitution, and it should be clear that we can do this quickly and efficiently for an upper-triangular matrix of any size. Furthermore, because we do at most one division per row, this method is very numerically stable. (If the matrix is ill-conditioned, we could still run into numerical error, but this only occurs when the original data set \(X\) suffers from multicollinearity.)

So hopefully you’re convinced by now that the \(QR\) form is desirable. But how do we calculate \(Q\) and \(R\)? There are two parts to understanding the algorithm. First, note that the product of any two orthogonal matrices is itself orthogonal. Also, the identity matrix is orthogonal. Therefore, if we have a candidate decomposition \(A = QR\) where \(Q\) is orthogonal (but R may not yet be square), then for any orthogonal matrix \(S\) we have \(A = Q I R = Q S^T S R = (Q S^T) (S R) = Q' R'\) where \(Q' = Q S^T\) and \(R' = S R\) is also a candidate decomposition! This is the general strategy behind not just QR decomposition, but behind many other decompositions in linear algebra: at each step we want to apply an orthogonal transformation designed to bring \(R\) closer to the desired form, while simultaneously keeping track of all the transformations applied so far in a single matrix \(Q\).

That sets the rules and the goal of the game: we can apply any sequence of orthogonal transforms to a (square, non-singular) matrix \(A\) that will bring it into upper triangular form. But what orthogonal transform will do that?

Householder Reflections

Let’s break it down into an even easier problem first. How would I make just one column of \(A\) zero below the diagonal? Or even more concretely, how would I make just the first column of \(A\) zero except for the first element?

Let’s take a look at the “column view” of our matrix. It looks like this:

\[ \begin{bmatrix} \vert & \vert & \vert \\ a_1 & a_2 & a_3 \\ \vert & \vert & \vert \end{bmatrix} \]

We want \(a_1\) to be zero except for the first element. What does that mean? Let’s call our basis vectors \(e_1 = [1\, 0\, 0]^T\), \(e_2 = [0\, 1\, 0]^T\), \(e_3 = [0\, 0\, 1]^T\). Every vector in our space is a linear combination of these basis vectors. So what it means for \(a_1\) to be zero except for the first element is that \(a_1\) is co-linear (in the same line) as \(e_1\): $ H a_i = e_i$.

We’re going to do this with an orthogonal transformation. But orthogonal transformations are length preserving. That means \(\alpha = ||a_1||\). Therefore we need to find an orthogonal matrix that sends the vector \(a_1\) to the vector \(||a_1|| e_1\). Note that any two vectors lie in a plane. We could either rotate by the angle between the vectors:

\[ \cos^{-1} \frac{a_1 \cdot e_1}{||a_1||} \]

or we can reflect across the line which bisects the two vectors in their plane. These two strategies are called the Givens rotation and the Householder reflection respectively. The rotation matrix is slightly less stable, so we will use the Householder reflection.

Let’s say that \(v\) is the unit normal vector of a plane; how would I reflect an arbitrary vector \(x\) across that plane? Well, if we subtracted \(\langle x, v \rangle v\) from \(x\), that would be a projection into the plane, right? So, if we just keep going the same direction and for the same distance again, we’ll end up a point on the other side of the plane \(x'\). Both \(x\) and \(x'\) project to the same point on the plane, and furthermore both are a distance \(\langle x, v \rangle\) from the plane. In other words, this operation is a reflection.

This diagram from Wikipedia illustrates this beautifully. Stare at it until you can see that reflecting about the dotted plane sends \(x\) to \(||x||e_1\), and believe that \(v\) is a unit vector orthogonal to the dotted plane of reflection.

Because a reflection is a linear transformation, we can express it as a matrix, which we will call \(H\). Here is how we go from our geometric intuition to a matrix:

\[ \begin{align} H x & \triangleq x - 2 \langle x, v \rangle v \\ & = x - 2v \langle x, v \rangle \\ & = Ix - 2 v (v^T x) \\ & = Ix - 2 (v v^T) x \\ & = (I - 2 (v v^T)) x \end{align} \]

Here, note that \(v v^T\) is the outer product of \(v\) with itself so is a square matrix with elements \(v_i v_j\). For example, if \(v = [\frac{1}{\sqrt{2}} \, \frac{1}{\sqrt{2}} \, 0]^T\) (the 45° line in the xy-plane) we get:

\[ H = I - 2 v v^T = \begin{bmatrix} 1 & 0 & 0 \\\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} - 2 \begin{bmatrix} \frac{1}{2} & \frac{1}{2} & 0 \\\ \frac{1}{2} & \frac{1}{2} & 0 \\ 0 & 0 & 0 \\ \end{bmatrix} = \begin{bmatrix} 0 & -1 & 0 \\\ -1 & 0 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} \]

We now know how to define reflections which zero out the subdiagonal of a target columns, and we know how to construct orthogonal matrices which perform that reflection.

Implementing the Lemmas

Given the above theoretical presentation, and copious inline comments, I hope you will now be able to read and understand the following code:

def householder_reflection(a, e):
    '''
    Given a vector a and a unit vector e,
    (where a is non-zero and not collinear with e)
    returns an orthogonal matrix which maps a
    into the line of e.
    '''
    
    # better safe than sorry.
    assert a.ndim == 1
    assert np.allclose(1, np.sum(e**2))
    
    # a and norm(a) * e are of equal length so
    # form an isosceles triangle. Therefore the third side
    # of the triangle is perpendicular to the line
    # that bisects the angle between a and e. This third
    # side is given by a - ||a|| e, which we will call u.
    # Since u lies in the plane spanned by a and e
    # its clear that u is actually orthogonal to a plane
    # equadistant to both a and ||a|| e. This is our
    # plane of reflection. We normalize u to v to 
    # because a unit vector is required in the next step.
    u = a - np.sign(a[0]) * np.linalg.norm(a) * e  
    v = u / np.linalg.norm(u)
    
    # derivation of the matrix form of a reflection:
    # x - 2<x, v>v ==
    # x - 2v<x, v> ==
    # Ix - 2 v (v^T x) ==
    # Ix - 2 (v v^T) x ==
    # (I - 2v v^T) x == H x
    H = np.eye(len(a)) - 2 * np.outer(v, v)
    
    return H

With the householder reflection in hand, we can implement an iterative version of the QR decomposition algorithm, using the Householder reflection on each column in turn to transform A into an upper triangular matrix.

def qr_decomposition(A):
    '''
    Given an n x m invertable matrix A, returns the pair:
        Q an orthogonal n x m matrix
        R an upper triangular m x m matrix
    such that QR = A.
    '''
    
    n, m = A.shape
    assert n >= m
    
    # Q starts as a simple identity matrix.
    # R is not yet upper-triangular, but will be.
    Q = np.eye(n)
    R = A.copy()
    
    # if the matrix is square, we can stop at m-1
    # because there are no elements below the pivot
    # in the last column to zero out. Otherwise we
    # need to do all m columns.
    for i in range(m - int(n==m)):
        # we don't actually need to construct it,
        # but conceptually we're working to update
        # the minor matrix R[i:, i:] during the i-th
        # iteration. 
        
        # the first column vector of the minor matrix.
        r = R[i:, i]
        
        # if r and e are already co-linear then we won't
        # be able to construct the householder matrix,
        # but the good news is we won't need to!
        if np.allclose(r[1:], 0):
            continue
            
        # e is the i-th basis vector of the minor matrix.
        e = np.zeros(n-i)
        e[0] = 1  
        
        # The householder reflection is only
        # applied to the minor matrix - the
        # rest of the matrix is left unchanged,
        # which we represent with an identity matrix.
        # Note that means H is in block diagonal form
        # where every block is orthogonal, therefore H
        # itself is orthogonal.
        H = np.eye(n)
        H[i:, i:] = householder_reflection(r, e)

        # QR = A is invariant. Proof:
        # QR = A, H^T H = I => 
        # Q H^T H R = A =>
        # Q' = Q H^T, R' = H R =>
        # Q' R' = A. QED.
        #
        # By construction, the first column of the 
        # minor matrix now has zeros for all
        # subdiagonal matrix. By induction, we 
        # have that all subdiagonal elements in
        # columns j<=i are zero. When i=N, R
        # is upper triangular. 
        Q = Q @ H.T
        R = H @ R
    
    return Q, R

The last piece of the puzzle is back-substitution. This is straightforward and available in standard libraries, but to comply with the letter-of-law of the “from scratch” challenge we’ll implement our own version.

def solve_triangular(A, b):
    '''
    Solves the equation Ax = b when A is an upper-triangular square matrix
    and b is a one dimensional vector by back-substitution. The length of b
    and the number of rows must match. Returns x as a one-dimensional numpy.ndarray
    of the same length as b.
    
    This isn't as micro-optimized as scipy.linalg.solve_triangular() but the
    algorithm is the same, and the asymptotic time complexity is the same.  
    '''
    
    # starting at the bottom, the last row is just a_N_N * x = b_N
    n, m = A.shape
    x = b[(m-1):m] / A[m-1, m-1]
    
    for i in range(m - 2, -1, -1):
        back_substitutions = np.dot(A[i, (i+1):], x)
        rhs = b[i] - back_substitutions
        x_i = rhs / A[i, i]  # possible ill-conditioning warning?
        x = np.insert(x, 0, x_i)
  
    return x

I won’t lie - that was a ton of linear algebra we just ploughed through. If you got through it, or if you had the good sense to skim ahead until you found something that made sense, congratulations.

Before we move on to actually using our new functions, let’s spend some time making sure everything up to this point is correct.

class QRTestCase(unittest.TestCase):
    '''
    Unit tests for QR decomposition and its dependencies. 
    '''
    
    def test_2d(self):
        A = np.array([[1,1], [0,1]])
        b = np.array([2,3])
        x = solve_triangular(A, b)
        assert_allclose(x, np.array([-1, 3]))
    
    def test_solve_triangular(self):
        for N in range(1, 20):
            A = np.triu(np.random.normal(size=(N, N)))
            x = np.random.normal(size=(N,))
            b = A @ x
            x2 = solve_triangular(A, b)
            assert_allclose(x, x2, atol=1e-5)

    def test_solve_rect_triangular(self):
        for N in range(1, 20):
            for N2 in [1, 5, 100]:
                A = np.triu(np.random.normal(size=(N+N2, N)))
                x = np.random.normal(size=(N,))
                b = A @ x
                x2 = solve_triangular(A, b)
                assert_allclose(x, x2, atol=1e-5)
     
    def test_reflection(self):
        x = np.array([1,1,1])
        e1 = np.array([1,0,0])
        H = householder_reflection(x, e1)
        assert_allclose(H @ (sqrt(3)* np.array([1, 0, 0])), x, atol=1e-5)
        assert_allclose(H @ np.array([1,1,1]), sqrt(3) * e1, atol=1e-5)
    
    def test_square_qr(self):
        # already upper triangular
        A = np.array([[2,1], [0, 3]])
        Q, R = qr_decomposition(A)
        assert_allclose(Q, np.eye(2))
        assert_allclose(R, A)
        
        N = 3
        Q = ortho_group.rvs(N) # generates random orthogonal matrices
        R = np.triu(np.random.normal(size=(N, N)))
        A = Q @ R
        Q2, R2 = qr_decomposition(Q @ R)
        # note that QR is not quite unique, so we can't
        # just test Q == Q2, unfortunately.
        assert_allclose(Q2 @ R2, Q @ R, atol=1e-5)
        assert_allclose(np.abs(det(Q2)), 1.0, atol=1e-5)
        assert_allclose(R2[2, 0], 0, atol=1e-5)
        assert_allclose(R2[2, 1], 0, atol=1e-5)
        assert_allclose(R2[1, 0], 0, atol=1e-5)
        
    def test_rect_qr(self):
        A = np.array([
            [2,1],
            [0,3],
            [4,5],
            [1,1],
        ])
        Q, R = qr_decomposition(A)
        assert_allclose(R[1:, 0], np.zeros(A.shape[0]-1), atol=1e-5)
        assert_allclose(R[2:, 0], np.zeros(A.shape[0]-2), atol=1e-5)
        assert_allclose(Q @ R, A, atol=1e-5)

unittest.main(argv=[''], exit=False)

With our trusty tools in hand, we’re ready to tackle linear regression properly.

Implementing Linear Regression

Recall that our problem was to solve the normal equation:

\[ X^T X \hat{\Theta} = X^T y \]

If we now let \(QR\) be the QR-decomposition of \(X\):

\[ (R^T Q^T)(Q R) \hat{\Theta} = R^T Q^T y \]

Since \(Q\) is orthogonal, \(Q^T Q = I\) and we can simplify this to:

\[ R^T R \hat{\Theta} = R^T Q^T y \]

For the next step, we have to assume the \(R\) is invertible. This is always the case if our original \(X\) was free of multicollinearity. It is also equivalent to \(X^T X\) being invertible so the naive approach of taking \((X^T X)^{-1}\) isn’t any stronger. Even gradient descent has issues with singular matrices because the problem is no longer strongly convex. There is a method based on SVD (singular value decomposition) which can handle linear regression in the presence of multicollinearity but it’s slower and in general the whole problem is better handled by removing redundant features or adding regularization, neither of which are in scope for this article.

A guy goes to the doctor and says, “Doctor, it hurts when I perform linear regression on a dataset with strong or perfect multicollinearity.” The doctor says, “don’t do that.”

In any case, let’s just assume that \(R^{-1}\) exists. We don’t actually have to calculate it, though! The mere fact of its existence lets us left multiply both sides of the equation by \((R^T)^{-1}\) and cancel the \(R^T\) on both sides, leaving only:

\[ R \hat{\Theta} = Q^T y \]

Because \(R\) is an upper triangular matrix, we can use our solve_triangular() function to solve this equation very quickly.

The final algorithm is deceptively simple. Compare the normal equations derived above to the final two lines of the fit() method.

class LinearRegression:
    def __init__(self, add_intercept=True):
        self.add_intercept = bool(add_intercept)

    def _design_matrix(self, X):
        if self.add_intercept:
            X = np.hstack([ np.ones((X.shape[0], 1)), X])
        return X

    def fit(self, X, y):
        X = self._design_matrix(X)
        Q, R = qr_decomposition(X)
        self.theta_hat = solve_triangular(R, Q.T @ y)
    
    def predict(self, X):
        X = self._design_matrix(X)
        return X @ self.theta_hat

Testing

Note that while we follow the scikit-learn naming conventions, up to this point we haven’t imported anything from sklearn. That’s in keeping with the “from scratch” challenge. However, to test the code, we are going to use a few sklearn and scipy dependencies.

Let’s first grab a bunch of test-only dependencies and also grab a copy of the famous Boston data set so we have a simple regression problem to play with.

# testing purposes only
from sklearn.datasets import load_boston
import matplotlib
from matplotlib import pyplot as plt
%matplotlib inline
from numpy.linalg import det
from scipy.stats import ortho_group
import unittest
from numpy.testing import assert_allclose

boston = load_boston()
X_raw = boston.data
y_raw = boston.target

# shuffle the data to randomize the train/test split
shuffle = np.random.permutation(len(y_raw))
X_full = X_raw[shuffle].copy()
y_full = y_raw[shuffle].copy()

# 80/20 train/test split. 
train_test_split = int(0.8 * len(y_full))
X_train = X_full[:train_test_split, :]
y_train = y_full[:train_test_split]
X_test = X_full[train_test_split:, :]
y_test = y_full[train_test_split:]

The model is fit to the training set only. If it fits the training set pretty well we know it has learned the examples we gave it; if it also fits the test set pretty well, we know it’s done more than just memorize the examples given but has also learned a more general lesson that it can apply to novel data that it’s never seen before.

A good way to visualize model performance is to plot \(y\) vs. \(\hat{y}\) - in other words, actual vs predicted. A perfect predictor would be a 45° diagonal through the origin; random guessing would be a shapeless or circular cloud of points.

model = LinearRegression()
model.fit(X_train, y_train)

def goodness_of_fit_report(label, model, X, y):
    y_hat = model.predict(X)
    
    # predicted-vs-actual plot
    plt.scatter(x=y, y=y_hat, label=label, alpha=0.5)
    plt.title("Predicted vs. Actual")
    plt.xlabel("Actual")
    plt.ylabel("Predictions")
    plt.legend()
    
    mse = np.mean( (y - y_hat)**2 )
    y_bar = np.mean(y)
    r2 = 1 - np.sum( (y-y_hat)**2 ) / np.sum( (y-y_bar)**2 )
    print("{label: <16} mse={mse:.2f}     r2={r2:.2f}".format(**locals()))
        
plt.figure(figsize=(16,6))
plt.subplot(1, 2, 1)
goodness_of_fit_report("Training Set", model, X_train, y_train)
plt.subplot(1, 2, 2)
goodness_of_fit_report("Test Set", model, X_test, y_test)

Training Set mse=21.30 r2=0.73

Test Set mse=25.12 r2=0.75

And in point of fact this linear regression model does reasonably well on both the train and test set, with correlation scores around 75%. That means it’s able to explain about three-quarters of the variation that it finds in \(y\) from what it was able to learn about the relationship between \(X\) and \(y\).

It’s also a good idea to visualize actual responses \(y\) and predictions \(\hat{y}\) as a function of the independent variables \(X\). In this case \(X\) is 13-dimensional so hard to visualized fully, so we will simply choose a few random pairs of dimensions dimensions so we can work in 2D. If the model has learned anything real about the relationship between \(X\) and \(y\), we should see two similar clouds of points for actual \(y\) and predicted \(\hat{y}\).

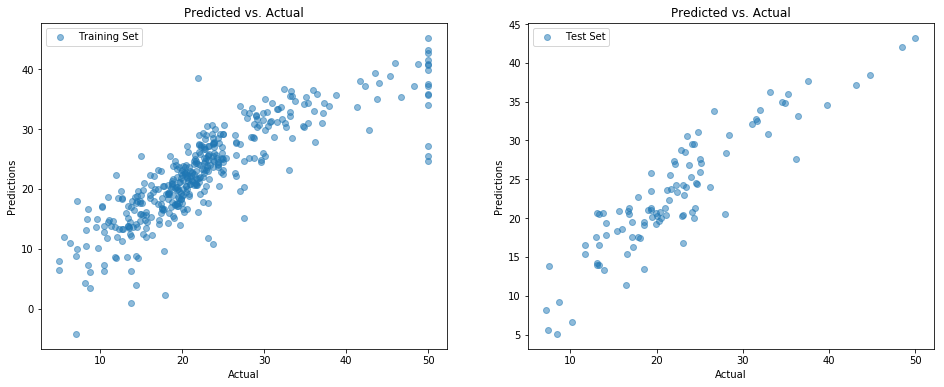
Prediction vs. Actual Scatterplot, training set and test set

We can also plot the actual and predicted response as a function of various predictors to get a sense of whether or not our function is truly fitting the data:

y_hat = model.predict(X_train)
plt.figure(figsize=(16,32))
for i in range(4, 8):
    plt.subplot(6, 2, i+1)
    plt.scatter(x=X_train[:, i], y=y_train, alpha=0.2, label='Actual')
    plt.scatter(x=X_train[:, i], y=y_hat, alpha=0.2, label='Predicted')
    plt.legend()
    plt.xlabel(boston.feature_names[i])
    plt.ylabel("Response Variable")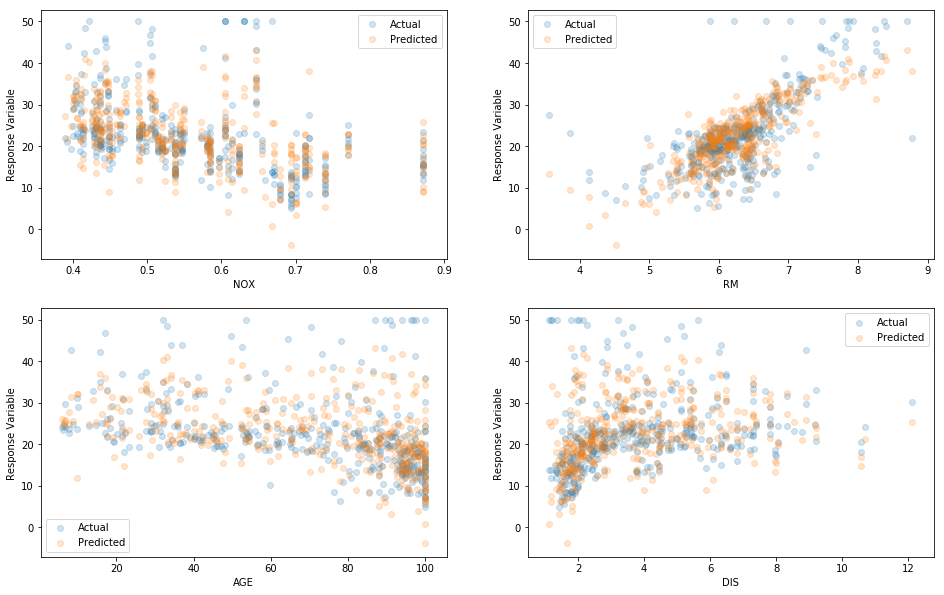

Predicted vs. Actual over pairs of independent variables

The eyeball test confirms that this model is fitting the data rather well, just as we’d expect when \(r^2 = 0.75\).

Conclusion

That was linear regression from scratch. There’s a lot more that could be said about linear regression even as a black box predictive model: polynomial and interaction terms, L1 and L2 regularization, and linear constraints on coefficients come to mind.

There’s also a whole universe of techniques for doing statistical modeling and inference with linear regression: testing residuals for homoscedasticity, normality, autocorrelation, variance inflation factors, orthogonal polynomial regression, Cook’s distance, leverage, Studentized residuals, ANOVA, AIC, BIC, Omnibus F-tests on nested models, etc., etc. Just to be clear, these aren’t variations or generalization of linear regression (although there are tons of those too) these are just standard techniques for analyzing and understanding linear regression models of the exact same form we calculated above. The topic is very mature and a huge amount of auxiliary mathematical machinery has been built up over the centuries (Gauss was studying OLS around 1800, and the problem is older than that.)

However, if we go too deeply into linear regression, we won’t get a chance to explore the rest of machine learning. So for the next part of the series, we will switch our attention to logistic regression and use that as an excuse to explore SGD in some detail. That will then serve as a jumping off point for our first “real” (or at least in fashion) machine learning algorithm in part 3: neural networks and backpropagation.